Machine-Learning Potentials for QM/MM
New challenges and possibilities for molecular dynamics simulations emerged with the rise of machine learning potentials (MLPs). MPLs can accelerate molecular dynamics simulations by orders of magnitude in comparison to ab-initio molecular dynamics (AIMD), but an efficient generation of relevant training data, their robustness in longer simulations and the transferability to different molecular systems remains challenging. Another challenge is the competition with semi-empirical methods, such as Density Functional Tight Binding (DFTB), which themselves accelerate calculations by orders of magnitude by parameterization.
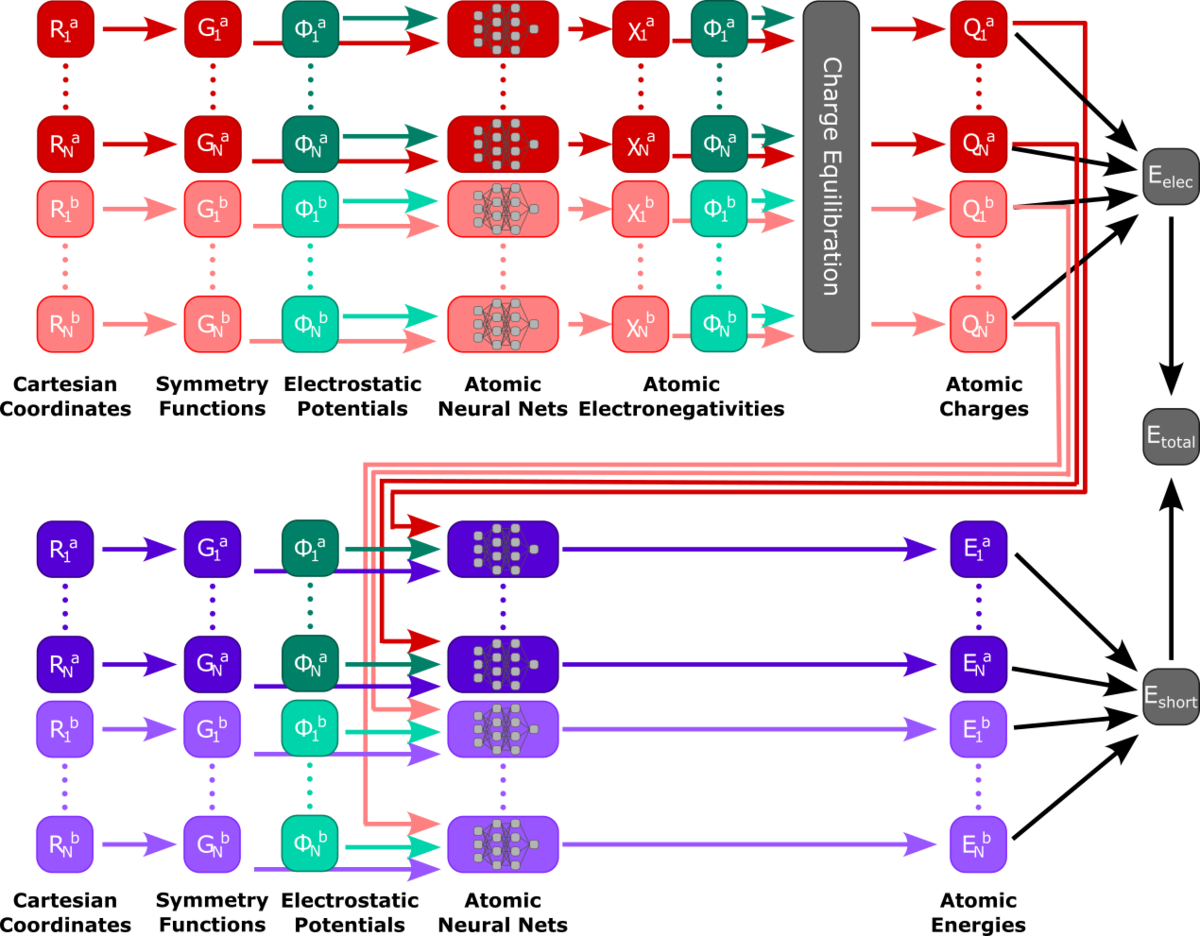
While MLP-driven simulations with thousands of atoms have already been performed, our approach for acceleration and precision is based on the QM/MM method. Instead of handing the whole system to the model, only the relevant part gets trained and evaluated by the model, while a suitable representation of the environment is included in the model inputs. By predicting energies and forces as a function of the QM atom positions and their environments the model can take the effects of a varying environment into account. The remaining environment gets handled by classical force field methods. Various methods ranging from simple dense neural networks to transferable High-Dimensional Neural Network Potentials and graph neural networks such as Schnet and MACE get applied for these methods.
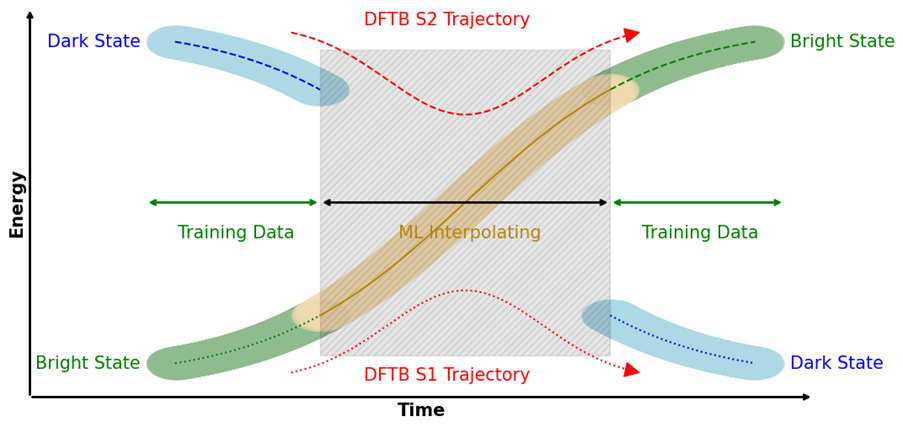
This approach is not only applicable for molecules in the ground state, but also for excited states. The accurate description of the behaviour in excited states is vital for the calculation of faithful fluorescence spectra. Tracking a specific bright state is a challenge for typical semi-empirical methods, whenever state crossing occurs. Training a neural network model on specifically selected data from the bright state can circumvent this problem, as the model is only aware of the bright state. The combination of a model predicting the dynamics of molecules in their excited state with a model predicting excited state properties like excitation energy and oscillator strength are the necessary tools for getting access to realistic fluorescence spectra.
The efficient sampling of non-redundant molecule conformations for a robust model is non-trivial. We primarily apply semi-empirical molecular dynamics simulations with enhanced sampling methods, such as metadynamics, as a sampling method. Further sampling methods in use include Normal Mode sampling, Principle Component Analysis based sampling and adaptive sampling. We integrate Normalizing Flow sampling and Wigner sampling into our repertoire.
References
- Gómez-Flores, C. L.; Maag, D.; Kansari, M.; Vuong, V.-Q.; Irle, S.; Gräter, F.; Kubař, T.; Elstner, M. Accurate Free Energies for Complex Condensed-Phase Reactions Using an Artificial Neural Network Corrected DFTB/MM Methodology. J. Chem. Theory Comput. 2022, 18 (2), 1213–1226.
- Behler, J.; Parrinello, M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98 (14), 146401.
- Ko, T. W.; Finkler, J. A.; Goedecker, S.; Behler, J. A Fourth-Generation High-Dimensional Neural Network Potential with Accurate Electrostatics Including Non-Local Charge Transfer. Nat. Commun. 2021, 12 (1), 398.
- Schütt, K. T.; Sauceda, H. E.; Kindermans, P.-J.; Tkatchenko, A.; Müller, K.-R. SchNet – A Deep Learning Architecture for Molecules and Materials. J. Chem. Phys. 2018, 148 (24), 241722.
- Batatia, I.; Kovacs, D. P.; Simm, G.; Ortner, C.; Csanyi, G. MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields. Adv. Neural Inf. Process. Syst. 2022, 35, 11423–11436.
| Name | Position | Portrait | |
|---|---|---|---|
| Dominik Hachenthal | Masterstudent | uxqck ∂does-not-exist.student kit edu | |
| Lukas Petersen | Ph.D. Student | lukas petersen ∂does-not-exist.kit edu | |
| 1 weitere Person ist nur innerhalb des KIT sichtbar. | |||